2024. 8. 19. 12:51ㆍMachine Learning/[TIL] Naver Boost Camp
what happens when $W=0$ init is used?
대칭성 문제: 모든 가중치를 0으로 초기화하면, 같은 층의 모든 뉴런들이 동일한 그래디언트를 받게 된다. 그 결과, 모든 뉴런이 동일한 방식으로 업데이트되고, 동일한 출력을 생성하게 된다. 이렇게 되면 뉴런들이 서로 다른 특성을 학습할 수 없게 되며, 각 뉴런의 역할이 중복된다.
그래디언트 전파 불가: 가중치가 0으로 초기화된 경우, 사용된 활성화 함수에 따라 역전파 과정에서 계산되는 그래디언트가 0이 될 수 있다.
First idea: Small Gaussian Random (평균이 0이고, 표준편차가 0.01인 정규분포=대부분 0 근처에 분포한다는 의미)
$W = 0.01 * np.random.randn(D,H)$
$tanh$함수의 입력값이 작으면, 출력이 거의 0에 가까워지는 상황이 발생한다.
$x ≈ 0$일 때, $tanh(Wx+b)$의 값이 거의 0에 가까워지며, 이로 인해 그래디언트도 거의 0이 됩니다.
그래디언트가 0에 가까워지면, 가중치 업데이트가 거의 이루어지지 않아서 신경망이 학습할 수 없게 됩니다.
작은 네트워크에서는 그럭저럭 작동할 수 있지만, 더 큰 네트워크에서는 각 층의 활성화 값(activations)이 균일하지 않은 분포를 나타낼 수 있다.
작은 네트워크의 경우: 작은 신경망에서는 가중치 초기화의 영향이 상대적으로 덜 중요하다. 층의 수가 적고, 파라미터의 수도 적기 때문에, 표준 편차가 0.01처럼 작은 값으로 가중치를 초기화해도 네트워크가 학습을 시작하는 데 큰 문제가 없을 수 있다. 작은 네트워크에서는 활성화 값이 각 층을 거치면서 극단적으로 커지거나 작아질 가능성이 낮습니다.
큰 네트워크의 경우: 네트워크가 커지고 층이 많아질수록 가중치 초기화의 효과는 매우 중요해진다. 만약 모든 가중치를 매우 작은 값으로 초기화하면, 각 뉴런의 출력(즉, 활성화 값)은 작아지게 된다. 이러한 작은 활성화 값이 여러 층을 거치면서 점점 더 작아지거나 그대로 유지되어, 역전파(backpropagation) 과정에서 신호가 약해진다. 이로 인해 네트워크가 효과적으로 학습하기 어려워진다.

Second idea:Large Gaussian Random
$W = 0.5 * np.random.randn(D,H)$
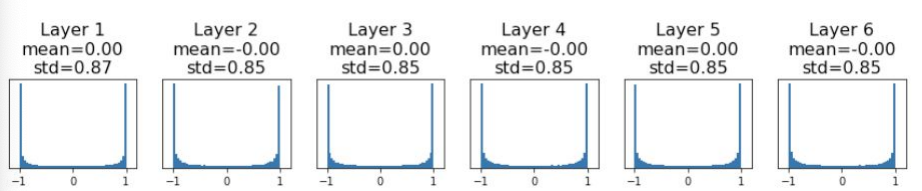
$tanh$함수의 입력값이 크면 출력이 ±1에 가깝게 포화되는 특성이 있다.
$tanh$의 출력이 ±1에 가까워지면,
$∂tanh(Wx+b)/∂W = 1 - tanh^2(Wx+b) \cdot x$가 0에 가까워지며, 이로 인해 그래디언트가 거의 0이 된다. 이 현상을 그래디언트 소실(Vanishing Gradient) 문제라고 부른다.
입력 값이 1 이상일 때, 모든 활성화 값이 ±1로 밀려버리고, 그로 인해 학습이 거의 이루어지지 않는다.
적절한 가중치 초기화 방법
“Xavier” Initialization”을 사용한다.
$W = np.random.randn(D,H) /np.sqrt(D)$
가중치를 $1/√D$으로 초기화 모든 층에서 활성화 값이 적절히 스케일되도록 한다. 즉, 네트워크의 깊이에 관계없이 각 층의 출력이 너무 크거나 작아지지 않도록 조정하는 것이 목표이다. 이 초기화 방법을 사용하면, 네트워크의 각 층에서 활성화 값들이 균일하게 분포되어, 그래디언트 소실(Vanishing Gradient) 문제나 그래디언트 폭발(Exploding Gradient) 문제를 줄일 수 있다.

ReLU와 Xavier 초기화의 비호환성Xavier 초기화는 ReLU 함수와 잘 맞지 않으며, 층이 깊어질수록 활성화 값이 0에 수렴하는 문제가 발생할 수 있다. 이는 그래디언트 소멸(Vanishing Gradient) 문제로 이어져, 네트워크가 학습을 제대로 하지 못하는 상황이 될 수 있다.

$W = np.random.randn(D,H) * np.sqrt(2/D)$Kaiming 초기화는 주로 ReLU와 같은 비선형 활성화 함수와 함께 사용되며, 네트워크의 모든 층에서 활성화 값이 적절히 분포되도록 하기 위해 설계되었다.
ReLU 함수가 양수 출력만을 허용하기 때문에, 이로 인해 발생할 수 있는 분산 감소를 보정하기 위해 가중치의 표준 편차를 $√(2 / D)$으로 설정한다.

[출처] cs2311n
'Machine Learning > [TIL] Naver Boost Camp' 카테고리의 다른 글
| Attention (0) | 2024.09.04 |
|---|---|
| [WEEK02-DAY2] 역전파의 전체 과정 (0) | 2024.08.19 |
| [WEEK02-DAY2] Zero-Centered Output (0) | 2024.08.19 |
| [WEEK02-DAY1] 최소 제곱법과 닫힌 형식 솔루션 (0) | 2024.08.19 |
| [WEEK02-DAY1] 선형 회귀 방정식 (0) | 2024.08.19 |